In order to survive and work under colder or hotter conditions, a warm climate at the skin surface must be provided by means of clothing as well as artificial heating or cooling. An understanding of the mechanisms of heat exchange through clothing is necessary to design the most effective clothing ensembles for work at extreme temperatures.

Clothing Heat Transfer Mechanisms

The nature of clothing insulation

Heat transfer through clothing, or conversely the insulation of clothing, depends largely on the air that is trapped in and on the clothing. Clothing consists, as a first approximation, of any sort of material that offers a grip to air layers. This statement is approximate because some material properties are still relevant. These relate to the mechanical construction of the fabrics (for instance wind resistance and the ability of fibres to support thick fabrics), and to intrinsic properties of fibres (for instance, absorption and reflection of heat radiation, absorption of water vapour, wicking of sweat). For not too extreme environmental conditions the merits of various fibre types are often overrated.

Air layers and air motion

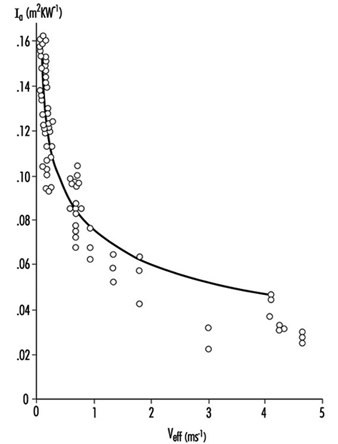
The notion that it is air, and in particular still air, that provides insulation, suggests that thick air layers are beneficial for insulation. This is true, but the thickness of air layers is physically limited. Air layers are formed by adhesion of gas molecules to any surface, by cohesion of a second layer of molecules to the first, and so on. However, the binding forces between subsequent layers are less and less, with the consequence that the outer molecules are moved by even tiny external motions of air. In quiet air, air layers may have a thickness up to 12 mm, but with vigorous air motion, as in a storm, the thickness decreases to less than 1 mm. In general there is a square-root relationship between thickness and air motion (see “Formulae and Definitions”). The exact function depends on the size and shape of the surface.

Heat conduction of still and moving air

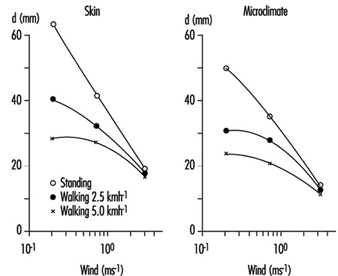
Still air acts as an insulating layer with a conductivity that is constant, regardless of the shape of the material. Disturbance of air layers leads to loss of effective thickness; this includes disturbances not only due to wind, but also due to the motions of the wearer of the clothing—displacement of the body (a component of wind) and motions of body parts. Natural convection adds to this effect. For a graph showing the effect of air velocity on the insulating ability of a layer of air, see figure 1.

Figure 1.  Effect of air velocity on insulating ability of an air layer.

Heat transfer by radiation

Radiation is another important mechanism for heat transfer. Every surface radiates heat, and absorbs heat that is radiated from other surfaces. Radiant heat flow is approximately proportional to the temperature difference between the two exchanging surfaces. A clothing layer between the surfaces will interfere with radiative heat transfer by intercepting the energy flow; the clothing will reach a temperature that is about the average of the temperatures of the two surfaces, cutting the temperature difference between them in two, and therefore the radiant flow is decreased by a factor of two. As the number of intercepting layers is increased, the rate of heat transfer is decreased.

Multiple layers are thus effective in reducing radiant heat transfer. In battings and fibre fleeces radiation is intercepted by distributed fibres, rather than a fabric layer. The density of the fibre material (or rather the total surface of fibre material per volume of fabric) is a critical parameter for radiation transfer inside such fibre fleeces. Fine fibres provide more surface for a given weight than coarse fibres.

Fabric insulation

As a result of the conductivities of enclosed air and radiation transfer, fabric conductivity is effectively a constant for fabrics of various thicknesses and bindings. The heat insulation is therefore proportional to the thickness.

Vapour resistance of air and fabrics

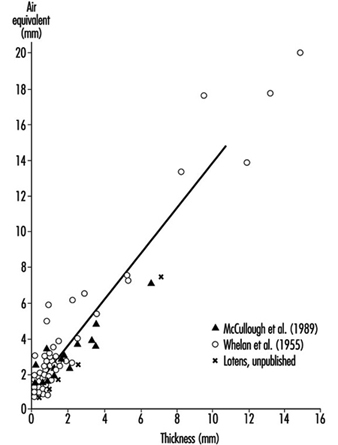
Air layers also create a resistance to the diffusion of evaporated sweat from humid skin to the environment. This resistance is roughly proportional to the thickness of the clothing ensemble. For fabrics, the vapour resistance is dependent on the enclosed air and the density of the construction. In real fabrics, high density and great thickness never go together. Due to this limitation it is possible to estimate the air equivalent of fabrics that do not contain films or coatings (see figure 8). Coated fabrics or fabrics laminated to films may have unpredictable vapour resistance, which should be determined by measurement.

Figure 2. Relationship between thickness and vapour resistance (deq) for fabrics without coatings.

From Fabric and Air Layers to Clothing

Multiple layers of fabric

Some important conclusions from the heat transfer mechanisms are that highly insulating clothing is necessarily thick, that high insulation may be obtained by clothing ensembles with multiple thin layers, that a loose fit provides more insulation than a tight fit, and that insulation has a lower limit, set by the air layer that adheres to the skin.

In cold-weather clothing it is often hard to obtain thickness by using thin fabrics only. A solution is to create thick fabrics, by mounting two thin shell fabrics to a batting. The purpose of the batting is to create the air layer and keep the air inside as still as possible. There is also a drawback to thick fabrics: the more the layers are connected, the stiffer the clothing becomes, thereby restricting motion.

Clothing variety

The insulation of a clothing ensemble depends to a large extent on the design of the clothing. Design parameters which affect insulation are number of layers, apertures, fit, distribution of insulation over the body and exposed skin. Some material properties such as air permeability, reflectivity and coatings are important as well. Furthermore, wind and activity change the insulation. Is it possible to give an adequate description of clothing for the purpose of prediction of comfort and tolerance of the wearer? Various attempts have been made, based on different techniques. Most estimates of complete ensemble insulation have been made for static conditions (no motion, no wind) on indoor ensembles, because the available data were obtained from thermal mannequins (McCullough, Jones and Huck 1985). Measurements on human subjects are laborious, and results vary widely. Since the mid-1980s reliable moving mannequins have been developed and used (Olesen et al. 1982; Nielsen, Olesen and Fanger 1985). Also, improved measurement techniques allowed for more accurate human experiments. A problem that still has not been overcome completely is proper inclusion of sweat evaporation in the evaluation. Sweating mannequins are rare, and none of them has a realistic distribution of sweat rate over the body. Humans sweat realistically, but inconsistently.

Definition of clothing insulation

Clothing insulation (I_cl in units of m²K/W) for steady state conditions, without radiation sources or condensation in the clothing, is defined in "Formulae and Definitions." Often I is expressed in the unit clo (not a standard international unit). One clo equals 0.155 m²K/W. The use of the unit clo implicitly means that it relates to the whole body and thus includes heat transfer by exposed body parts.

I is modified by motion and wind, as explained earlier, and after correction the result is called resultant insulation. This is a frequently used but not generally accepted term.

Distribution of clothing over the body

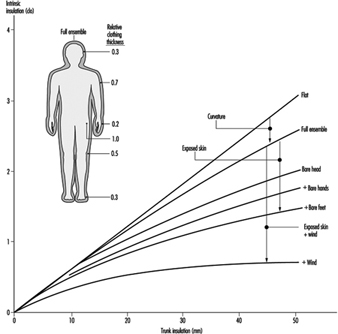
Total heat transfer from the body includes heat that is transferred by exposed skin (usually head and hands) and heat passing through the clothing. Intrinsic insulation (see "Formulae and Definitions") is calculated over the total skin area, not only the covered part. Exposed skin transfers more heat than covered skin and thus has a profound influence on the intrinsic insulation. This effect is enhanced by increasing wind speed. Figure 3 shows how the intrinsic insulation decreases successively due to curvature of body shapes (outer layers less effective than inner), exposed body parts (additional pathway for heat transfer) and increased wind speed (less insulation, in particular for exposed skin) (Lotens 1989). For thick ensembles the reduction in insulation is dramatic.

Figure 3. Intrinsic insulation, as it is influenced by body curvature, bare skin and wind speed.

Typical ensemble thickness and coverage

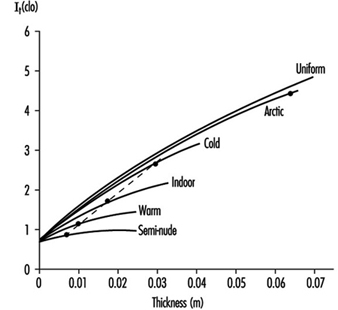
Apparently both the insulation thickness and the skin coverage are important determinants of heat loss. In real life the two are correlated in the sense that winter clothing is not only thicker, but also covers a larger proportion of the body than summer wear. Figure 4 demonstrates how these effects together result in an almost linear relation between clothing thickness (expressed as volume of insulation material per unit of clothing area) and insulation (Lotens 1989). The lower limit is set by the insulation of the adjacent air and the upper limit by usability of the clothing. Uniform distribution may provide the best insulation in the cold, but it is impractical to have much weight and bulk on the limbs. Therefore the emphasis is often on the trunk, and the sensitivity of local skin to cold is adapted to this practice. Limbs play an important role in controlling human heat balance, and high insulation of the limbs limits the effectiveness of this regulation.

Figure 4. Total insulation resulting from clothing thickness and distribution over the body.

Ventilation of clothing

Trapped air layers in the clothing ensemble are subject to motion and wind, but to a different degree than the adjacent air layer. Wind creates ventilation in the clothing, both as air penetrating the fabric and by passing through apertures, while motion increases internal circulation. Havenith, Heus and Lotens (1990) found that inside clothing, motion is a stronger factor than in the adjacent air layer. This conclusion is dependent on the air permeability of the fabric, however. For highly air-permeable fabrics, ventilation by wind is considerable. Lotens (1993) showed that ventilation can be expressed as a function of effective wind speed and air permeability.

Estimates of Clothing Insulation and Vapour Resistance

Physical estimates of clothing insulation

Thickness of a clothing ensemble provides a first estimate of insulation. Typical conductivity of an ensemble is 0.08 W/mK. At an average thickness of 20 mm, that results in an I_cl of 0.25 m²K/W, or 1.6 clo. However, loose-fitting parts, such as trousers or sleeves, have a much higher conductivity, more on the order of 0.15, whereas tightly packed clothing layers have a conductivity of 0.04, the famous 4 clo per inch reported by Burton and Edholm (1955).

Estimates from tables

Other methods use table values for clothing items. These items have been measured previously on a mannequin. An ensemble under investigation has to be separated into its components, and these have to be looked up in the table. Making an incorrect choice of the most similar tabulated clothing item may cause errors. In order to obtain the intrinsic insulation of the ensemble, the single insulation values have to be put in a summation equation (McCullough, Jones and Huck 1985).

Clothing surface area factor

In order to calculate total insulation, f_cl has to be estimated (see "Formulae and Definitions"). A practical experimental estimate is to measure the clothing surface area, make corrections for overlapping parts, and divide by total skin area (DuBois and DuBois 1916). Other estimates from various studies show that f_cl increases linearly with intrinsic insulation.

Estimate of vapour resistance

For a clothing ensemble, vapour resistance is the sum of resistance of air layers and clothing layers. Usually the number of layers varies over the body, and the best estimate is the area-weighted average, including exposed skin.

Relative vapour resistance

Evaporative resistance is less frequently used than I, because few measurements of C_cl (or P_cl) are available. Woodcock (1962) avoided this problem by defining the water vapour permeability index i_m as the ratio of I and R, related to the same ratio for a single air layer (this latter ratio is nearly a constant and known as the psychrometric constant S, 0.0165 K/Pa, 2.34 Km³/g or 2.2 K/torr); i_m= I/(R·S). Typical values for i_m for non-coated clothing, determined on mannequins, are 0.3 to 0.4 (McCullough, Jones and Tamura 1989). Values for i_m for fabric composites and their adjacent air can be measured relatively simply on a wet hotplate apparatus, but the value is actually dependent on air flow over the apparatus and the reflectivity of the cabinet in which it is mounted. Extrapolation of the ratio of R and I for clothed humans from measurements on fabrics to clothing ensembles (DIN 7943-2 1992) is sometimes attempted. This is a technically complicated matter. One reason is that R is proportional only to the convective part of I, so that careful corrections have to be made for radiative heat transfer. Another reason is that trapped air between fabric composites and clothing ensembles may be different. In fact, vapour diffusion and heat transfer can be better treated separately.

Estimates by articulated models

More sophisticated models are available to calculate insulation and water vapour resistance than the above-explained methods. These models calculate local insulation on the basis of physical laws for a number of body parts and integrate these to intrinsic insulation for the whole human shape. For this purpose the human shape is approximated by cylinders (figure ). The model by McCullough, Jones and Tamura (1989) requires clothing data for all layers in the ensemble, specified per body segment. The CLOMAN model of Lotens and Havenith (1991) requires fewer input values. These models have similar accuracy, which is better than any of the other methods mentioned, with the exception of experimental determination. Unfortunately and inevitably the models are more complex than would be desirable in a widely accepted standard.

Figure 5. Articulation of human shape in cylinders.

Effect of activity and wind

Lotens and Havenith (1991) also provide modifications, based on literature data, of the insulation and vapour resistance due to activity and wind. Insulation is lower while sitting than standing, and this effect is larger for highly insulating clothing. However, motion decreases insulation more than posture does, depending on the vigour of the movements. During walking both arms and legs move, and the reduction is larger than during cycling, when only the legs move. Also in this case, the reduction is larger for thick clothing ensembles. Wind decreases insulation the most for light clothing and less for heavy clothing. This effect might relate to the air permeability of the shell fabric, which is usually less for cold-weather gear.

Figure 8 shows some typical effects of wind and motion on vapour resistance for rainwear. There is no definite agreement in the literature about the magnitude of motion or wind effects. The importance of this subject is stressed by the fact that some standards, such as ISO 7730 (1994), require resultant insulation as an input when applied for active persons, or persons exposed to significant air motion. This requirement is often overlooked.

Figure 6. Decrease in vapour resistance with wind and walking for various rainwear.

Moisture Management

Effects of moisture absorption

When fabrics can absorb water vapour, as most natural fibres do, clothing works as a buffer for vapour. This changes the heat transfer during transients from one environment to another. As a person in non-absorbing clothing steps from a dry to a humid environment, the evaporation of sweat decreases abruptly. In hygroscopic clothing the fabric absorbs vapour, and the change in evaporation is only gradual. At the same time the absorption process liberates heat in the fabric, increasing its temperature. This reduces the dry heat transfer from the skin. In first approximation, both effects cancel each other, leaving the total heat transfer unchanged. The difference with non-hygroscopic clothing is the more gradual change in evaporation from the skin, with less risk of sweat accumulation.

Vapour absorption capacity

Absorption capacity of fabric depends on the fibre type and the fabric mass. Absorbed mass is roughly proportional to the relative humidity, but is higher above 90%. The absorption capacity (called regain) is expressed as the amount of water vapour that is absorbed in 100 g of dry fibre at the relative humidity of 65%. Fabrics can be classified as follows:

• low absorption—acrylic, polyester (1 to 2 g per 100 g)
• intermediate absorption—nylon, cotton, acetate (6 to 9 g per 100 g)
• high absorption—silk, flax, hemp, rayon, jute, wool (11 to 15 g per 100 g).

Water uptake

Water retention in fabrics, often confused with vapour absorption, obeys different rules. Free water is loosely bound to fabric and spreads well sideways along capillaries. This is known as wicking. Transfer of liquid from one layer to another takes place only for wet fabrics and under pressure. Clothing may be wetted by non-evaporated (superfluous) sweat that is taken up from the skin. The liquid content of fabric may be high and its evaporation at a later moment a threat to the heat balance. This typically happens during rest after hard work and is known as after-chill. The ability of fabrics to hold liquid is more related to fabric construction than to fibre absorption capacity, and for practical purposes is usually sufficient to take up all the superfluous sweat.

Condensation

Clothing may get wet by condensation of evaporated sweat at a particular layer. Condensation occurs if the humidity is higher than the local temperature allows. In cold weather that will often be the case at the inside of the outer fabric, in extreme cold even in deeper layers. Where condensation takes place, moisture accumulates, but the temperature increases, as it does during absorption. The difference between condensation and absorption, however, is that absorption is a temporary process, whereas condensation may continue for extended times. Latent heat transfer during condensation may contribute very significantly to heat loss, which may or may not be desirable. The accumulation of moisture is mostly a drawback, because of discomfort and risk of after-chill. For profuse condensation, the liquid may be transported back to the skin, to evaporate again. This cycle works as a heat pipe and may strongly reduce the insulation of the underclothing.

Dynamic Simulation

Since the early 1900s many standards and indices have been developed to classify clothing and climates. Almost without exception these have dealt with steady states—conditions in which the climate and work were maintained long enough for a person to develop a constant body temperature. This type of work has become rare, due to improved occupational health and work conditions. The emphasis has shifted to short-duration exposure to harsh circumstances, often related to calamity management in protective clothing.

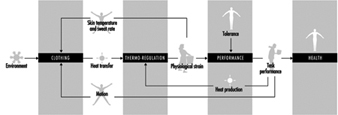
There is thus a need for dynamic simulations involving clothing heat transfer and thermal strain of the wearer (Gagge, Fobelets and Berglund 1986). Such simulations can be carried out by means of dynamic computer models that run through a specified scenario. Among the most sophisticated models to date with respect to clothing is THDYN (Lotens 1993), which allows for a wide range of clothing specifications and has been updated to include individual characteristics of the simulated person (figure 9). More models may be expected. There is a need, however, for extended experimental evaluation, and running such models is the work of experts, rather than the intelligent layperson. Dynamic models based on the physics of heat and mass transfer include all heat transfer mechanisms and their interactions—vapour absorption, heat from radiant sources, condensation, ventilation, moisture accumulation, and so on—for a wide range of clothing ensembles, including civil, work and protective clothing.

Figure 7. General description of a dynamic thermal model.

Back