Ionizing radiation is everywhere. It arrives from outer space as cosmic rays. It is in the air as emissions from radioactive radon and its progeny. Naturally occurring radioactive isotopes enter and remain in all living things. It is inescapable. Indeed, all species on this planet evolved in the presence of ionizing radiation. While humans exposed to small doses of radiation may not immediately show any apparent biological effects, there is no doubt that ionizing radiation, when given in sufficient amounts, can cause harm. These effects are well known both in kind and in degree.

While ionizing radiation can cause harm, it also has many beneficial uses. Radioactive uranium generates electricity in nuclear power plants in many countries. In medicine, x rays produce radiographs for diagnosis of internal injuries and diseases. Nuclear medicine physicians use radioactive material as tracers to form detailed images of internal structures and to study metabolism. Therapeutic radiopharmaceuticals are available to treat disorders such as hyperthyroidism and cancer. Radiotherapy physicians use gamma rays, pion beams, electron beams, neutrons and other types of radiation to treat cancer. Engineers use radioactive material in oil well logging operations and in soil moisture density gauges. Industrial radiographers use x rays in quality control to look at internal structures of manufactured devices. Exit signs in buildings and aircraft contain radioactive tritium to make them glow in the dark in the event of a power failure. Many smoke detectors in homes and commercial buildings contain radioactive americium.

These many uses of ionizing radiation and radioactive materials enhance the quality of life and help society in many ways. The benefits of each use must always be compared with the risks. The risks may be to workers directly involved in applying the radiation or radioactive material, to the public, to future generations and to the environment or to any combination of these. Beyond political and economic considerations, benefits must always outweigh risks when ionizing radiation is involved.

Ionizing Radiation

Ionizing radiation consists of particles, including photons, which cause the separation of electrons from atoms and molecules. However, some types of radiation of relatively low energy, such as ultraviolet light, can also cause ionization under certain circumstances. To distinguish these types of radiation from radiation that always causes ionization, an arbitrary lower energy limit for ionizing radiation usually is set around 10 kiloelectron volts (keV).

Directly ionizing radiation consists of charged particles. Such particles include energetic electrons (sometimes called negatrons), positrons, protons, alpha particles, charged mesons, muons and heavy ions (ionized atoms). This type of ionizing radiation interacts with matter primarily through the Coulomb force, repelling or attracting electrons from atoms and molecules by virtue of their charges.

Indirectly ionizing radiation consists of uncharged particles. The most common kinds of indirectly ionizing radiation are photons above 10 keV (x rays and gamma rays) and all neutrons.

X-ray and gamma-ray photons interact with matter and cause ionization in at least three different ways:

1. Lower-energy photons interact mostly via the photoelectric effect, in which the photon gives all of its energy to an electron, which then leaves the atom or molecule. The photon disappears.
2. Intermediate-energy photons mostly interact through the Compton effect, in which the photon and an electron essentially collide as particles. The photon continues in a new direction with reduced energy while the released electron goes off with the remainder of the incoming energy (less the electron’s binding energy to the atom or molecule).
3. Pair production is possible only for photons with energy in excess of 1.02 MeV. (However, near 1.02 MeV, the Compton effect still dominates. Pair production dominates at higher energies.) The photon disappears and an electron-positron pair appears in its place (this occurs only in the vicinity of a nucleus because of conservation of momentum and energy considerations). The total kinetic energy of the electron-positron pair is equal to the energy of the photon less the sum of the rest-mass energies of the electron and positron (1.02 MeV). These energetic electrons and positrons then proceed as directly ionizing radiation. As it loses kinetic energy, a positron will eventually encounter an electron, and the particles will annihilate each other. Two (usually) 0.511 MeV photons are then emitted from the annihilation site at 180 degrees from each other.

a given photon any of these can occur, except that pair production is possible only for photons with energy greater than 1.022 MeV. The energy of the photon and the material with which it interacts determine which interaction is the most likely to occur.

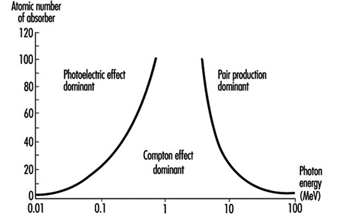
Figure 1 shows the regions in which each type of photon interaction dominates as a function of photon energy and atomic number of absorber.

Figure 1. Relative importance of the three principal interactions of photons in matter

The most common neutron interactions with matter are inelastic collisions, neutron capture (or activation) and fission. All of these are interactions with nuclei. A nucleus colliding inelastically with a neutron is left at a higher energy level. It can release this energy in the form of a gamma ray or by emitting a beta particle, or both. In neutron capture, an affected nucleus may absorb the neutron and eject energy as gamma or x rays or beta particles, or both. The secondary particles then cause ionization as discussed above. In fission, a heavy nucleus absorbs the neutron and splits into two lighter nuclei that are almost always radioactive.

Quantities, Units and Related Definitions

The International Commission on Radiation Units and Measurements (ICRU) develops internationally accepted formal definitions of quantities and units of radiation and radioactivity. The International Commission on Radiological Protection (ICRP) also sets standards for definition and use of various quantities and units used in radiation safety. A description of some quantities, units and definitions commonly used in radiation safety follows.

Absorbed dose. This is the fundamental dosimetric quantity for ionizing radiation. Basically, it is the energy ionizing radiation imparts to matter per unit mass. Formally,

where D is the absorbed dose, de is the mean energy imparted to matter of mass dm. Absorbed dose has units of joules per kilogram (J kg^–1). The special name for the unit of absorbed dose is the gray (Gy).

Activity. This quantity represents the number of nuclear transformations from a given nuclear energy state per unit time. Formally,

where A is the activity, dN is the expectation value of the number of spontaneous nuclear transitions from the given energy state in the time interval dt. It is related to the number of radioactive nuclei N by:

where l is the decay constant. Activity has units of inverse seconds (s^–1). The special name for the unit of activity is the becquerel (Bq).

Decay constant (l). This quantity represents the probability per unit time that a nuclear transformation will occur for a given radionuclide. The decay constant has units of inverse seconds (s^–1). It is related to the half-life t_½ of a radionuclide by:

The decay constant l is related to the mean lifetime, t, of a radionuclide by:

The time dependence of activity A(t) and of the number of radioactive nuclei N(t) can be expressed by and  respectively.

Deterministic biological effect. This is a biological effect caused by ionizing radiation and whose probability of occurrence is zero at small absorbed doses but will increase steeply to unity (100%) above some level of absorbed dose (the threshold). Cataract induction is an example of a stochastic biological effect.

Effective dose. The effective dose E is the sum of the weighted equivalent doses in all the tissues and organs of the body. It is a radiation safety quantity, so its use is not appropriate for large absorbed doses delivered in a relatively short period of time. It is given by:

where w _T is the tissue weighting factor and H_T is the equivalent dose for tissue T. Effective dose has units of J kg^–1. The special name for the unit of effective dose is the sievert (Sv).

Equivalent dose. The equivalent dose H_T is the absorbed dose averaged over a tissue or organ (rather than at a point) and weighted for the radiation quality that is of interest. It is a radiation safety quantity, so its use is not appropriate for large absorbed doses delivered in a relatively short period of time. The equivalent dose is given by:

where D_T,R is the absorbed dose averaged over the tissue or organ T due to radiation R and w _R
is the radiation weighting factor. Equivalent dose has units of J kg^–1. The special name for the unit of equivalent dose is the sievert (Sv).

Half-life. This quantity is the amount of time required for the activity of a radionuclide sample to reduce by a factor of one-half. Equivalently, it is the amount of time required for a given number of nuclei in a given radioactive state to reduce by a factor of one-half. It has fundamental units of seconds (s), but is also commonly expressed in hours, days and years. For a given radionuclide, half-life t_½ is related to the decay constant l by:

Linear energy transfer. This quantity is the energy a charged particle imparts to matter per unit length as it traverses the matter. Formally,

where L is the linear energy transfer (also called linear collision stopping power) and de is the mean energy lost by the particle in traversing a distance dl. Linear energy transfer (LET) has units of J m^–1.

Mean lifetime. This quantity is the average time a nuclear state will survive before it undergoes a transformation to a lower energy state by emitting ionizing radiation. It has fundamental units of seconds (s), but may also be expressed in hours, days or years. It is related to the decay constant by:

where t is the mean lifetime and l is the decay constant for a given nuclide in a given energy state.

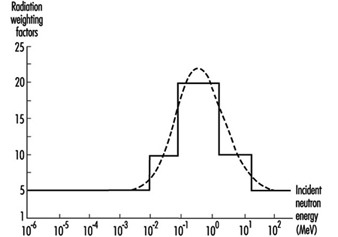
Radiation weighting factor. This is a number w _R that, for a given type and energy of radiation R, is representative of values of the relative biological effectiveness of that radiation in inducing stochastic effects at low doses. The values of w _R are related to linear energy transfer (LET) and are given in table 1. Figure 2 (overleaf) shows the relationship between w _R and LET for neutrons.

Table 1. Radiation weighting factors w_R

¹ All values relate to the radiation incident on the body or, for internal sources, emitted from the source.

² Excluding Auger electrons emitted from nuclei bound to DNA.

Relative biological effectiveness (RBE). The RBE of one type of radiation compared with another is the inverse ratio of the absorbed doses producing the same degree of a defined biological end point.

Figure 2. Radiation weighting factors for neutrons (the smooth curve is to be treated  as an approximation)

Stochastic biological effect. This is a biological effect caused by ionizing radiation whose probability of occurrence increases with increasing absorbed dose, probably with no threshold, but whose severity is independent of absorbed dose. Cancer is an example of a stochastic biological effect.

Tissue weighting factor w _T. This represents the contribution of tissue or organ T to the total detriment due to all of the stochastic effects resulting from uniform irradiation of the whole body. It is used because the probability of stochastic effects due to an equivalent dose depends on the tissue or organ irradiated. A uniform equivalent dose over the whole body should give an effective dose numerically equal to the sum of effective doses for all tissues and organs of the body. Therefore, the sum of all tissue weighting factors is normalized to unity. Table 2 gives values for tissue weighting factors.

Table 2. Tissue weighting factors w_T

¹ The values have been developed from a reference population of equal numbers of both sexes and a wide range of ages. In the definition of effective dose they apply to workers, to the whole population, and to either sex.

² For purposes of calculation, the remainder is composed of the following additional tissues and organs: adrenals, brain, upper large intestine, small intestine, kidneys, muscle, pancreas, spleen, thymus and uterus. The list includes organs that are likely to be selectively irradiated. Some organs in the list are known to be susceptible to cancer induction.

³ In those exceptional cases in which a single one of the remainder tissues or organs receives an equivalent dose in excess of the highest dose in any of the twelve organs for which a weighting factor is specified, a weighting factor of 0.025 should be applied to that tissue or organ and a weighting factor of 0.025 to the average dose in the rest of the remainder as defined above.

Back